Консультация для педагогов дошкольных образовательных учреждений на тему «Использование кругов Эйлера для развития связной речи дошкольников, имеющих тяжёлые нарушения речи».
методическая разработка по логопедии (подготовительная группа) по теме

Консультация предназначена для воспитателей, учителей-логопедов дошкольных образовательных учреждений.

Скачать:

Вложение	Размер
icpolzovanie_krugov_eylera_dlya_razvitiya_svyaznoy_rechi.docx	636.07 КБ

Предварительный просмотр:

Консультация для педагогов дошкольных образовательных учреждений на тему

«Использование кругов Эйлера для развития связной речи дошкольников, имеющих тяжёлые нарушения речи».

Для развития связной речи детей, имеющих тяжёлые нарушения речи, я использую круги Эйлера.

Круги Эйлера – это геометрическая схема, с помощью которой можно наглядно отобразить отношения между понятиями или множествами объектов. Они были изобретены Леонардом Эйлером в 18 веке и с тех пор широко используются в математике, логике и в различных прикладных направлениях. Учитывая простоту и наглядность модели кругов Эйлера, она может быть с успехом использована в детском саду на занятиях по развитию речи. Признаки предмета в кругах Эйлера обозначаю схематично, с помощью пиктограмм.

Круги Эйлера могут с успехом использоваться в детском саду как в непосредственно образовательной деятельности в образовательных областях «Коммуникация», «Познание», «Социализация»,
так и в самостоятельной деятельности детей. Используя круги Эйлера ребенок учится сопоставлять, обобщать, группировать материал в целях запоминания, развивается речь, память и мышление.

Я в своей работе с дошкольниками для развития логического мышления при классификации использую модель «классификационного древа» и кругов Эйлера, которые наглядно отражают родовидовые отношения.

В развитии навыка составления описательных рассказов большую помощь оказывает предварительное составление модели описания. В процессе обучения связной описательной речи моделирование может служить средством и программой анализа и фиксации закономерных свойств и отношений объекта или явления.
Основу описательного рассказа составляют конкретные представления, накапливаемые в процессе исследования объекта описания. Элементами модели описательного рассказа становятся символы-заместители качественных характеристик объекта:
• принадлежность к родовидовому понятию;
• величина;
• цвет;
• форма;
• составляющие детали;
• качество поверхности;
• материал, из которого изготовлен объект (для неживых предметов);
• как он используется (какую пользу приносит)?
• за что нравится (не нравится)?
По данной модели возможно составить описание отдельного предмета, принадлежащего к определенной группе.
Овладение приемом сравнительного описания происходит, когда дети научатся свободно оперировать моделью описания отдельных предметов или явлений. Два-три ребенка или подгруппы детей составляют модель описания двух и более предметов по плану. При этом символы описания (пиктограммы) выкладываются каждой подгруппой в свой обруч. Затем в пересечении обручей (круги Эйлера) выделяются одинаковые признаки предметов. Дети сравнивают предметы, определяя сначала их сходство, а затем различия.

Для развития связной речи, овладение приемом сравнительного описания на логопедических занятиях с детьми, имеющими тяжёлые речевые нарушения я использую заранее нарисованные схемы, круги Эйлера. Различие предметов указаны схематично в кругах, сходства, одинаковые признаки предметов, указаны в пересечении колец.

Карточка-схема для сравнительного описания апельсина и лимона.

Иллюстрация из авторского архива

Сравнительное описание апельсина и лимона.

Апельсин и лимон это фрукты. Они растут на деревьях. Перед тем как их съесть их нужно хорошо помыть водой. Они очень полезны для человека. В них много витаминов. У этих фруктов много общего, но также есть и отличия. Апельсин по цвету — оранжевый, а лимон – жёлтый. Апельсин круглый, а лимон овальный. Апельсин сладкий, а лимон – кислый. Апельсин можно вымыть и съесть, можно из апельсинов выжать апельсиновый сок. С лимоном можно пить чай.

Карточка-схема для сравнительного описания кошки и собаки.

Иллюстрация из авторского архива

Сравнительное описание кошки и собаки.

Кошка и собака – это домашние животные. О них заботится человек. Он их кормит, ухаживает за ними. Тело кошки и собаки покрыто шерстью. У этих животных есть голова, туловище, уши, хвост, лапы. У кошки – кошачий, а у собаки – собачий хвост. Кошка коричневого цвета, а собака – рыжего. Кошка мяукает, а собака – лает. Кошка любит пить молоко и есть рыбу, а собака грызть кости. Кошка и собака приносят пользу человеку. Собака охраняет дом, а кошка ловит мышей.

См. в приложении

Сравнительное описание кошки и собаки.

Сравнительное описание лисы и зайца.
Сравнительное описание перчаток и рукавиц.

Сравнительное описание апельсина и лимона.

Сравнительное описание кувшина и кружки.

Сравнительное описание барабана и трубы.

Сравнительное описание футболки и свитера.

1. КорвяковаН. Ф. Применение пиктограмм в работе с детьми с особыми потребностями // Проблемы патологии развития и распада речевой функции. – СПб., 1999.
2. Лалаева Р. И., СеребряковаН. В. Формирование лексики и грамматического строя у дошкольников с общим недоразвитием ре-чи. – СПб.,2001.
3. Развитие опосредованной памяти при заучивании стихов с помощью зрительных опор [Текст]/ М.Н. Бакаева// Логопед. — 2011. — № 7. – 120с.

По теме: методические разработки, презентации и конспекты

В приложении представлены карточки для составления рассказов по разным лексическим темам.

Работа предназначена для воспитателей, учителей-логопедов, родителей.

В коррекционной работе по развитию фонематических представлений мною активно используется метод наглядного моделирования. Одним из средств повышения ум.

Проблемы речи детей дошкольного возраста:Односложная, состоящая лишь из простых предложений речь. Неспособность грамматически правильно построить предложение.Бедность речи. Недостаточный с.

Цель мастер класса:Повышение профессиональной компетентности педагогов в использовании инновационной игровой технологии- круги Эйлера при организации работы с детьми по развитию логического мышления.

Материал содержит цели, задачи, этапы работы.

Цель мастер класса: Повышение профессиональной компетентности педагогов в использовании инновационной игровой технологии– круги Эйлера при организации работы с детьми по развитию логическог.

Решение логических задач и силлогизмов , страница 2

2) Живая вода находится в красном или синем сосуде;

3) В жёлтом сосуде находится живая или обычная вода;

4) Если окажется, что в красном сосуде живая вода, то в желтом будет мёртвая.

В каком сосуде какая вода, если допустить, что записка правдива?

Живая вода находится в синем сосуде, поскольку если бы она оказа­лась в красном, то в желтом, согласно правдивой записке, находилась бы мер­твая вода, а это противоречило бы утверждению, что в желтом сосуде либо живая, вода либо обычная. Таким образом, в желтом сосуде – обычная вода, а в красном — мертвая.

7. г) В поисках принцессы, похищенной Кощеем, Иванушка оказался в старинном замке. Пре­о­до­лев массу препятствий, он очутился в помещении, из которого вели три двери. Иванушка знал, что за какой-то из них находится принцесса, за другой сидит тигр, а за оставшейся дверью никого нет. На дверях были вид­ны надписи:

На 1-ой: Здесь нет ни принцессы, ни тигра;

На 2-ой: За 3-ей дверью никого нет;

На 3-ей: Здесь находится принцесса.

Все надписи были ложными, их сделал Кощей, чтобы ввести Иванушку в заблуж­де­ние.

За какой дверью находится принцесса?

Методом исключения можно выяснить, что за 3-й дверью находится тигр, поскольку два пункта ложной записки говорят о том, что именно за 3-й дверью «находится принцесса» и «никого нет». Принцессу Кощей спрятал за 1-й дверью, поскольку тигра за ней точно нет и никого не быть там не мо­жет. Следовательно, за 2-й дверью никого нет.

1. Решите задачи, приведённые в учебнике Гетмановой на стр. 54.

II. Определить отношения между следующими понятиями:

1 Законченная поветь, незаконченная повесть.

Несовместимые противоречащие понятия.

2. Строение, дом, деревянный дом, беседка, недостроенное строение.

3. Трусливый человек, нетрусливый человек.

Несовместимые противоречащие понятия.

4. Карлик, великан.

Несовместимые противоречащие понятия.

5. Университет, биологический факультет.

7. Мать, дочь, бабушка, внучка, сестра.

8. Населенный пункт, город, город на Днепре, столица, Город Украины.

9. Спутник планеты, естественный спутник, спутник Земли, Луна, спутник Юпитера, Марс.

10. Пожар, причина пожара, взрыв атомной бомбы, поджог, молния.

III Подобрать понятия, отношения между которыми изображаются кругами Эй­ле­ра так:

1) A – студенты,

2)

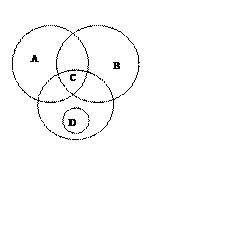
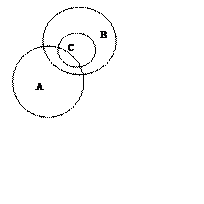
При помощи диаграмм Эйлера-Венна графически изобразить отно­ше­ния между понятиями:

2)

D – женщины;

Решение задач с помощью кругов Эйлера

Классы: 5 , 6 , 7

Ключевые слова: круги Эйлера

Пояснительная записка

Очень часто решение задачи помогает найти рисунок. Использование рисунка делает решение простым и наглядным.

В данной разработке приведены примеры решения задач с помощью кругов Эйлера. Это не просто занимательная и интересная штука, но и весьма полезный метод решения задач. Они помогают быстро и просто решить даже достаточно сложные или просто запутанные на первый взгляд задачи.

С данным способом решения задач учащихся можно познакомить как на уроках, так и на кружковых занятиях.

Главной целью этой работы является помощь учителям математики для подготовки учащихся к олимпиадам, а также к экзаменам.

Основные понятия

Понятие множества − одно из первичных в математике. Поэтому очень трудно дать ему какое-либо определение, которое бы не заменяло слово «множество» каким-нибудь равнозначным выражением, например, совокупность, собрание элементов и т.д. Элементы множества − это то, из чего это множество состоит, например, каждый ученик вашего класса есть элемент множества школьников.

Пересечение множеств в теории множеств — это множество, которому принадлежат те и только те элементы, которые одновременно принадлежат всем данным множествам.

Круги Эйлера — геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления. Изобретены Леонардом Эйлером. Используется в математике, логике, менеджменте и других прикладных направлениях.

2. Решение задач с помощью кругов Эйлера

2.1. «Обитаемый остров» и «Стиляги»

Некоторые ребята из нашего класса любят ходить в кино. Известно, что 15 ребят смотрели фильм «Обитаемый остров», 11 человек — фильм «Стиляги», из них 6 смотрели и «Обитаемый остров», и «Стиляги». Сколько человек смотрели только фильм «Стиляги»?

Решение:

Чертим два множества таким образом:

6 человек, которые смотрели фильмы «Обитаемый остров» и «Стиляги», помещаем в пересечение множеств.

1. 15 — 6 = 9 — человек, которые смотрели только «Обитаемый остров»,

2. 11- 6 = 5 — человек, которые смотрели только «Стиляги».

Ответ: 5 человек.

2.2. Задача про библиотеки

Каждый из 35 шестиклассников является читателем, по крайней мере, одной из двух библиотек: школьной и районной. Из них 25 человек берут книги в школьной библиотеке, 20 — в районной.

1. Являются читателями обеих библиотек;
2. Не являются читателями районной библиотеки;
3. Не являются читателями школьной библиотеки;
4. Являются читателями только районной библиотеки;
5. Являются читателями только школьной библиотеки?

Решение:

Чертим два множества таким образом:

1) 20+ 25 — 35 = 10 (человек) — являются читателями обеих библиотек. На схеме это общая часть кругов. Мы определили единственную неизвестную нам величину. Теперь, глядя на схему, легко даем ответы на поставленные вопросы.

2) 35 — 20 = 15 (человек) — не являются читателями районной библиотеки,

3) 35 — 25 = 10 (человек) — не являются читателями школьной библиотеки,

4) 35- 20 = 10 (человек) — являются читателями только районной библиотеки,

5) 35- 20 = 15 (человек) — являются читателями только школьной библиотеки.

Очевидно, что вопросы 2 и 5, а также 3 и 4 — равнозначны и ответы на них совпадают.

Ответ: 10 человек; 15 человек; 10 человек; 10 человек; 15 человек.

2.3. Гарри Поттер, Рон и Гермиона

На полке стояло 26 волшебных книг по заклинаниям, все они были прочитаны. Из них 4 прочитал и Гарри Поттер, и Рон. Гермиона прочитала 7 книг, которых не читали ни Гарри Поттер, ни Рон, и две книги, которые читал Гарри Поттер. Всего Гарри Поттер прочитал 11 книг. Сколько книг прочитал только Рон?

Решение:

Учитывая условия задачи, сделаем чертеж:

Так как Гарри Поттер всего прочитал 11 книг, из них 4 книги читал Рон и 2 книги — Гермиона, то 11 — 4 — 2 = 5 — книг прочитал только Гарри.

Следовательно, 26 — 7 — 2 — 5 — 4 = 8 — книг прочитал только Рон.

Ответ: 8 книг.

2.4. Задача про любимые мультфильмы

Шестиклассники заполняли анкету с вопросами об их любимых мультфильмах. Оказалось, что большинству из них нравятся «Белоснежка и семь гномов», «Губка Боб Квадратные Штаны» и «Волк и теленок». В классе 38 учеников. «Белоснежка и семь гномов» нравится 21 ученику. Причем трем среди них нравятся еще и «Волк и теленок», шестерым — «Губка Боб Квадратные Штаны», а один ребенок одинаково любит все три мультфильма. У «Волка и теленка» 13 фанатов, пятеро из которых назвали в анкете два мультфильма. Надо определить, скольким же шестиклассникам нравится «Губка Боб Квадратные Штаны».

Решение:

Чертим три круга, таким образом:

Из условия знаем, что трем ученикам нравиться и «Белоснежка и семь гномов», и «Волк и теленок», шестерым — «Белоснежка и семь гномов» и «Губка Боб Квадратные Штаны», а один ребенок одинаково любит все три мультфильма.

Мы помним, что по условиям задачи среди фанатов мультфильма «Волк и теленок» пятеро ребят выбрали два мультфильма сразу, т.е. 5 — 3 = 2 — ученика выбрали «Волк и теленок» и «Губка Боб Квадратные Штаны».

1) 21 — 3 — 1 — 6 = 11 — учеников выбрали только «Белоснежка и семь гномов»,

2) 13 — 3 — 1 — 2 = 7 — учеников выбрали — «Волк и теленок»,

3) 38 — (11 + 3 + 1 + 2 + 6 + 7) = 8 — ребят выбрали «Губка Боб Квадратные Штаны».

4) 8 + 2 + 1 + 6 = 17 — человек выбрали мультик «Губка Боб Квадратные Штаны».

Ответ: 17 учеников.

2.5. Задача про Крейсер и Линкор

В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети интернет.

Найдено страниц, тыс.

Крейсер и Линкор

Какое количество страниц (в тысячах) будет найдено по запросу Крейсер и Линкор? (Считается, что все вопросы выполняются практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.)

Решение:

При помощи кругов Эйлера изобразим условия задачи.

1) 4800 + 4500 — 7000 = 2300 (тыс. страниц) — найдено по запросу Крейсер и Линкор,

2) 4800 — 2300 = 2500 (тыс. страниц) — найдено по запросу Крейсер,

3) 4500 — 2300 = 2200 (тыс. страниц) — найдено по запросу Линкор.

Ответ: 2300 тыс. страниц.

2.6. Задача про блондинок

Каждый ученик класса — либо девочка, либо блондин, либо любит математику. В классе 20 девочек, из них 12 блондинок, но одна блондинка любит математику. Всего в классе 24 ученика — блондина, математику из них любят 12, а всего учеников (мальчиков и девочек), которые любят математику, 17, из них 6 девочек. Сколько учеников в данном классе?

Решение:

Изобразим с помощью кругов Эйлера данные из задачи:

1) 12 — 1 = 11 (учеников) — девочек блондинок,

2) 12 — 1 = 11 (учеников) — блондины и любят математику,

3) 6 — 1 = 5 (учеников) — девочек, которые любят математику,

4) 20 — 11 — 1 — 5 = 3 (ученика) — девочки,

5) 24 — 11 — 1 — 11 = 1 (ученик) — блондин,

6) 17- 5 — 1 — 11 = 0 (учеников) — любят математику,

7) 3 + 1 + 0 + 5 + 11 + 11 + 1 = 32 (ученика) — всего в классе.

Ответ: 32 ученика.

2.7. Задача про кружки

В трёх седьмых классах 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют в хоре, не увлекаются спортом и не занимаются в драмкружке? Сколько ребят заняты только спортом?

Решение:

Учитывая условия задачи, сделаем чертеж:

1) 10 — 3 = 7 (ребят) — посещают драмкружок и хор,

2) 6 — 3 = 3 (ребят) — поют в хоре и занимаются спортом,

3) 8 — 3 = 5 (ребят) — занимаются спортом и посещают драмкружок,

4) 27 — 7 — 3 — 5 = 12 (ребят) — посещают драмкружок,

5) 32 — 7 3 — 3 = 19 (ребят) — поют в хоре,

6) 22 — 5 — 3 — 3 = 11 (ребят) — увлекаются спортом,

7) 70 — (12 + 19 + 11 + 5+ 7 + 3 + 3) = 10 (ребят) — не поют в хоре, не увлекаются спортом и не занимаются в драмкружке.

Ответ: 10 человек и 11 человек.

Задачи для самостоятельного решения

1. На фирме работают 67 человек. Из них 47 знают английский язык, 35 — немецкий язык, а 23 — оба языка. Сколько человек фирмы не знают ни английского, ни немецкого языков?

2. Из 40 учащихся нашего класса 32 любят молоко, 21 — лимонад, а 15 — и молоко, и лимонад. Сколько ребят в нашем классе не любят ни молоко, ни лимонад?

3. 12 моих одноклассников любят читать детективы, 18 — фантастику, трое с удовольствием читают и то, и другое, а один вообще ничего не читает. Сколько учеников в нашем классе?

4. Из тех 18 моих одноклассников, которые любят смотреть триллеры, только 12 не прочь посмотреть и мультфильмы. Сколько моих одноклассников смотрят одни «мультики», если всего в нашем классе 25 учеников, каждый из которых любит смотреть или триллеры, или мультфильмы, или и то и другое?

5. Из 29 мальчишек нашего двора только двое не занимаются спортом, а остальные посещают футбольную или теннисную секции, а то и обе. Футболом занимается 17 мальчишек, а теннисом — 19. Сколько футболистов играет в теннис? Сколько теннисистов играет в футбол?

6. В одном классе 25 учеников. Из них 7 любят груши, 11 — черешню. Двое любят груши и черешню; 6 — груши и яблоки; 5 — яблоки и черешню. Но есть в классе два ученика, которые любят все и четверо таких, что не любят фруктов вообще. Сколько учеников этого класса любят яблоки?

7. В конкурсе красоты участвовали 22 девушки. Из них 10 было красивых, 12 — умных и 9 — добрых. Только 2 девушки были и красивыми, и умными; 6 девушек были умными и одновременно добрыми. Определите, сколько было красивых и в то же время добрых девушек, если я скажу вам, что среди участниц не оказалось ни одной умной, доброй и вместе с тем красивой девушки?

8. В нашем классе 35 учеников. За первую четверть пятерки по русскому языку имели 14 учеников; по математике — 12; по истории — 23. По русскому и математике — 4; по математике и истории — 9; по русскому языку и истории — 5. Сколько учеников имеют пятерки по всем трем предметам, если в классе нет ни одного ученика, не имеющего пятерки хотя бы по одному из этих предметов?

9. Из 100 человек 85 знают английский язык, 80 — испанский, 75 — немецкий. Все владеют, по крайней мере, одним иностранным языком. Среди них нет таких, которые знают два иностранных языка, но есть владеющие тремя языками. Сколько человек из этих 100 знают три языка?

10. Из сотрудников фирмы 16 побывали во Франции, 10 — в Италии, 6 — в Англии; в Англии и Италии — 5; в Англии и Франции — 6; во всех трех странах — 5 сотрудников. Сколько человек посетили и Италию, и Францию, если всего в фирме работают 19 человек, и каждый из них побывал хотя бы в одной из названных стран?

Список использованных источников

1. Баженов И.И, Порошкин А.Г., Тимофеев А.Ю., Яковлев В.Д. Задачи для школьных математических кружков: учеб. пособие / Сыктывкар: Сыктывкарский университет, 2006.

2. Марков И.С. Новые олимпиады по математике — Ростов н/Д: Феникс, 2005.